CSC 411
During this course, students will gain understanding of research over the course of a long-term project that will take them a year. This course is closely associated with CSC 421.
Project allocation
The allocation of projects done by solving a a Mixed Integer Linear Programming problem defined by balancing the needs of
- each student, expressed as preference for 10 projects. 1 denotes first choice, 10 denotes last choice and
- each lecturer, expressed a preference for his/her project where 1 denotes first choice, etc.
The assignment is done in a way that minimises an objective function (called "unhappiness") of the form: 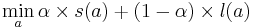 , where the scores (
, where the scores (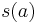 for student scores and
for student scores and 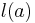 for lecturer scores) are calculated from the assignments (
for lecturer scores) are calculated from the assignments ( ) and the preferences.
) and the preferences. 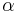 is chosen to favour the students (it is currently 0.95).
is chosen to favour the students (it is currently 0.95).
Certain constraints have to be taken into account:
- each student must get a project
- lecturers have a minimum and maximum number of projects (usually 3 and 5 with some exceptions)
- projects have a minimum and maximum number of students. These are normally 0 and 1, but some projects may be assigned to more than one student.
These constraints mean that the objective function may be larger than the optimal assignment without these constraints. In rare cases this may force some students to get a project they have not chosen assigned to them.
In addition, as there are many equivalent solutions that have the same objective function value in terms of student unhappines, the aggregate mark for each student is used as a "tie breaker". A sensitivity analysis is performed to see the effect of varying tweaks on the student unhappiness, and most tweaks are only allowed if they do not affect the student unhappiness.