UP student number checksum
UP student number checksum
The last digit of UP student numbers is a check digit, calculated according to the similar rules as an ISBN 10. ISBN 10 check digit is calculated "so that multiplying each digit by its position in the number (counting from the right) and taking the sum of these products modulo 11 is 0" (from Wikipedia). It appears as though the UP check digit does not have a similarly easy check for validity, although the calculation of the check digit is similar up to a point.
The sum
To calculate the check digit for a 7 digit student number, follow this procedure. Take the first digit and multiply by 8, the second by 7, the third by 6 and so on:
| Digit | 9 | 7 | 0 | 0 | 8 | 0 | 4 |
| i | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| Product | 72 | 49 | 0 | 0 | 32 | 0 | 8 |
Add the products together and call this 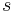 . In the example above,
. In the example above, 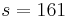 The check digit is now
The check digit is now 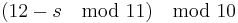 . For the example, we would get
. For the example, we would get 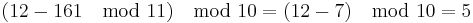 .
.
Code
Awk
This awk program recognises short student numbers at the beginnig of lines and replaces the first field with the long student number
/^s[0-9][0-9][0-9][0-9][0-9][0-9][0-9]/ {
split($1, digits, "");
s = 0
for (i=2; i<9; i++)
s += digits[i] * (10-i);
$1 = $1 (12 - (s % 11)) % 10
}
{print}
Python
This python function calculates the check digit of a short student number passed as a string:
def checkdigit(short): # Calculate check digit s = sum(int(char)*(8-i) for i,char in enumerate(short)) return (12 - (s % 11)) % 10
Basic
This Basic function (suitable for calls from MS Excel or OpenOffice Calc), calculates the check digit:
function checkdigit(numstr as variant) as integer
' calculates the check digit (8th number) of a 7 digit student number
dim i, s as integer
s = 0
for i = 1 to 7
s = s + CInt(mid(numstr, i, 1))*(9-i)
next i
checkdigit = (12 - (s mod 11)) mod 10
end function