Difference between revisions of "CPN 321"
From Chemical Engineering @ UP wiki
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | This page provides supplementary information regarding the CPD 320 Process Dynamics module. The bulk of material for this module is hosted on ClickUP and is accessible if you are registered for the module. | ||
| + | |||
| + | The dynamic behaviour of chemical processing units plays an important role in the modelling and control of these processes. This module serves as an introduction to process dynamics where emphasis is placed on the time dependent behaviour of processes, rather than steady state applications of continuity equations. The aim of this module is to enable the student to: | ||
| + | * understand and use the principles governing the dynamic behaviour of processes | ||
| + | * set up mathematical models that describe the time-dependent behaviour of processes | ||
| + | * solve the mathematical models to obtain a time response for given changes in the system | ||
| + | * evaluate and examine different time-responses using basic computer programming | ||
| + | * to understand the basics of a feedback control loop. | ||
| + | |||
| + | == Related Modules == | ||
| + | Prerequisite knowledge: [[CRV 210]], [[MPR 210]] | ||
| + | This subject is tightly coupled to [[CPB 410]] | ||
| + | |||
| + | == Study Themes == | ||
| + | === Modelling: development of a process model from basic principles === | ||
| + | * Construct dynamic mass, energy and component balances that describe the time-dependent changes within a process. | ||
| + | * Choose a set of state variables that fully describes a certain chemical process. | ||
| + | * Be able to identify and use relationships (fundamental or empirical) between process variables other than the conservation laws. | ||
| + | * Understand that the mass, energy or component accumulation terms will give rise to a differential term in the dynamic conservation equations (dynamic mass, energy or component balances). | ||
| + | * Understand that the dynamic conservation equations will be differential equations. | ||
| + | * Identify the role of variables in the system, ie input, output, state, dependant, independent variables and parameters of the system. | ||
| + | * Fully specify the description of a process so that the degrees of freedom are zero for the system before an attempt is made to solve the system of equations. | ||
| + | * Define inputs or specify control relationships to ensure that the degrees of freedom of the process are zero. | ||
| + | * Understand the concept of steady state in a continuous system and how the steady state can be disturbed by an input change, giving rise to time-dependent behaviour. | ||
| + | * Understand what a dynamic (time-dependent) response means. | ||
| + | * Employ vector and matrix notation to simplify model expressions. | ||
| + | * Solve simple differential equations (from a process model) analytically (after appropriate linearisation) to determine how the output variables change with respect to time for a given input disturbance/change. | ||
| + | |||
| + | === Simulation: Solving the model equations === | ||
| + | |||
| + | * Distinguish between the different problems of simulation: linear equations, nonlinear equations, ODEs, DAEs and PDEs | ||
| + | * Use linear algebra to solve sets of linear algebraic equations | ||
| + | * Use a root-finding algorithm (like Newton’s method) to solve sets of nonlinear algebraic equations, as for determination of steady state. | ||
| + | * Use an integration algorithm (like Euler’s method) to solve a set of differential equations. | ||
| + | * Use built-in functions in Octave to solve these problems. | ||
| + | * Implement their own programs in Octave to solve these problems. | ||
| + | * Obtain the response of the output variables of a process after a given input disturbance and to repreent this graphically. | ||
| + | * Examine how the different process parameters influence the dynamic response of a process. | ||
| + | * Determine under what conditions will a process reach a new steady state after a given input disturbance. | ||
| + | |||
| + | === Linearisation of non-linear systems and deviation variables === | ||
| + | |||
| + | * identify linear and non-linear terms in a differential equation. | ||
| + | * approximate non-linear differential equations as linear differential equations by linearising the non-linear terms in the equation around a selected reference condition using a first-order Taylor series expansion. | ||
| + | * rewrite a linear differential equation or linearised differential equation in deviation variable form. | ||
| + | |||
| + | === Laplace transforms and transfer functions === | ||
| + | |||
| + | * Solve ordinary linear differential equations by transforming to the Laplace domain and understand why the deviation variable form of the differential equations is advantageous when applying the Laplace transform and inverting the result back to the time domain. | ||
| + | * Understand the use of transfer functions to represent dynamic systems in a block diagram and how transfer functions represents the differential equations describing a system. | ||
| + | * Represent multiple transfer functions in a block diagram | ||
| + | * Analysis in the Laplace domain | ||
| + | |||
| + | === Dynamic behaviour of linear systems === | ||
| + | |||
| + | * Distinguish between first, second and higher-order systems | ||
| + | * Rewrite differential equations into standard form to identify the following parameters: Steady-state Gain (sensitivity), time constant & damping coefficient. | ||
| + | * Understand the effect of each of these parameters on the dynamic behaviour of a process | ||
| + | * Understand how the poles of a system relate to the time constants, damping coefficient and stability of the system. | ||
| + | * Explain the phenomenon of inverse response and how that is represented in the Laplce domain. | ||
| + | * The origin and effect of dead time and how this is represented in the Laplace domain. | ||
| + | |||
| + | === The elements of the feedback control loop === | ||
| + | |||
| + | * Distinguish between open and closed loop systems and to develop the closed loop transfer function for setpoint and for load disturbances. . | ||
| + | * Identify the elements of the feedback control loop and how the hardware of a feedback control loop function are linked to each other (process, disturbance, transmitters, measuring elements, controller (with comparator) and final control element (control valves) | ||
| + | * Identify the controlled variable, the manipulated variable and the disturbance or load variable for a specific system given the control objective(s). | ||
| + | * Distinguish between the principle of feedback and feedforward control action. | ||
| + | * Represent the feedback control loop in block format and realise that the variables are represented as deviation variables. | ||
| + | * The principle of operation of each of the three terms of the PID-controller algorithm, namely Proportional, Integral & Derivative. | ||
| + | * The concept of direct acting & reverse acting controllers | ||
| + | * Understand the difference between servo and regulatory control | ||
| + | * Clearly understand that the roots of the characteristic equation (like the poles of any transfer function) contain information on the stability and shape of the servo and regulatory responses. | ||
| + | * Understand that the controller parameters (Kc, <math>\tau_I</math>, <math>\tau_D</math>) determine what the roots of the characteristic equation of the closed-loop system will be. | ||
| + | |||
| + | === Process identification and parameter estimation: obtaining a dynamic process model using experimental measurements === | ||
| + | |||
| + | * understand the underlying requirements when using input disturbances to obtain a process model from the process response. | ||
| + | * obtain a process model making use of a step input and the process reaction curve. | ||
| + | |||
| + | == Simulation Project == | ||
| + | Have a look at [[CPD320 Simulation Project|this page]] for help with common problems regarding the simulation project. | ||
| + | |||
[[Category:Modules|3rd Year]] | [[Category:Modules|3rd Year]] | ||
Latest revision as of 05:42, 13 July 2017
This page provides supplementary information regarding the CPD 320 Process Dynamics module. The bulk of material for this module is hosted on ClickUP and is accessible if you are registered for the module.
The dynamic behaviour of chemical processing units plays an important role in the modelling and control of these processes. This module serves as an introduction to process dynamics where emphasis is placed on the time dependent behaviour of processes, rather than steady state applications of continuity equations. The aim of this module is to enable the student to:
- understand and use the principles governing the dynamic behaviour of processes
- set up mathematical models that describe the time-dependent behaviour of processes
- solve the mathematical models to obtain a time response for given changes in the system
- evaluate and examine different time-responses using basic computer programming
- to understand the basics of a feedback control loop.
Contents
- 1 Related Modules
- 2 Study Themes
- 2.1 Modelling: development of a process model from basic principles
- 2.2 Simulation: Solving the model equations
- 2.3 Linearisation of non-linear systems and deviation variables
- 2.4 Laplace transforms and transfer functions
- 2.5 Dynamic behaviour of linear systems
- 2.6 The elements of the feedback control loop
- 2.7 Process identification and parameter estimation: obtaining a dynamic process model using experimental measurements
- 3 Simulation Project
Related Modules
Prerequisite knowledge: CRV 210, MPR 210 This subject is tightly coupled to CPB 410
Study Themes
Modelling: development of a process model from basic principles
- Construct dynamic mass, energy and component balances that describe the time-dependent changes within a process.
- Choose a set of state variables that fully describes a certain chemical process.
- Be able to identify and use relationships (fundamental or empirical) between process variables other than the conservation laws.
- Understand that the mass, energy or component accumulation terms will give rise to a differential term in the dynamic conservation equations (dynamic mass, energy or component balances).
- Understand that the dynamic conservation equations will be differential equations.
- Identify the role of variables in the system, ie input, output, state, dependant, independent variables and parameters of the system.
- Fully specify the description of a process so that the degrees of freedom are zero for the system before an attempt is made to solve the system of equations.
- Define inputs or specify control relationships to ensure that the degrees of freedom of the process are zero.
- Understand the concept of steady state in a continuous system and how the steady state can be disturbed by an input change, giving rise to time-dependent behaviour.
- Understand what a dynamic (time-dependent) response means.
- Employ vector and matrix notation to simplify model expressions.
- Solve simple differential equations (from a process model) analytically (after appropriate linearisation) to determine how the output variables change with respect to time for a given input disturbance/change.
Simulation: Solving the model equations
- Distinguish between the different problems of simulation: linear equations, nonlinear equations, ODEs, DAEs and PDEs
- Use linear algebra to solve sets of linear algebraic equations
- Use a root-finding algorithm (like Newton’s method) to solve sets of nonlinear algebraic equations, as for determination of steady state.
- Use an integration algorithm (like Euler’s method) to solve a set of differential equations.
- Use built-in functions in Octave to solve these problems.
- Implement their own programs in Octave to solve these problems.
- Obtain the response of the output variables of a process after a given input disturbance and to repreent this graphically.
- Examine how the different process parameters influence the dynamic response of a process.
- Determine under what conditions will a process reach a new steady state after a given input disturbance.
Linearisation of non-linear systems and deviation variables
- identify linear and non-linear terms in a differential equation.
- approximate non-linear differential equations as linear differential equations by linearising the non-linear terms in the equation around a selected reference condition using a first-order Taylor series expansion.
- rewrite a linear differential equation or linearised differential equation in deviation variable form.
Laplace transforms and transfer functions
- Solve ordinary linear differential equations by transforming to the Laplace domain and understand why the deviation variable form of the differential equations is advantageous when applying the Laplace transform and inverting the result back to the time domain.
- Understand the use of transfer functions to represent dynamic systems in a block diagram and how transfer functions represents the differential equations describing a system.
- Represent multiple transfer functions in a block diagram
- Analysis in the Laplace domain
Dynamic behaviour of linear systems
- Distinguish between first, second and higher-order systems
- Rewrite differential equations into standard form to identify the following parameters: Steady-state Gain (sensitivity), time constant & damping coefficient.
- Understand the effect of each of these parameters on the dynamic behaviour of a process
- Understand how the poles of a system relate to the time constants, damping coefficient and stability of the system.
- Explain the phenomenon of inverse response and how that is represented in the Laplce domain.
- The origin and effect of dead time and how this is represented in the Laplace domain.
The elements of the feedback control loop
- Distinguish between open and closed loop systems and to develop the closed loop transfer function for setpoint and for load disturbances. .
- Identify the elements of the feedback control loop and how the hardware of a feedback control loop function are linked to each other (process, disturbance, transmitters, measuring elements, controller (with comparator) and final control element (control valves)
- Identify the controlled variable, the manipulated variable and the disturbance or load variable for a specific system given the control objective(s).
- Distinguish between the principle of feedback and feedforward control action.
- Represent the feedback control loop in block format and realise that the variables are represented as deviation variables.
- The principle of operation of each of the three terms of the PID-controller algorithm, namely Proportional, Integral & Derivative.
- The concept of direct acting & reverse acting controllers
- Understand the difference between servo and regulatory control
- Clearly understand that the roots of the characteristic equation (like the poles of any transfer function) contain information on the stability and shape of the servo and regulatory responses.
- Understand that the controller parameters (Kc,
, 
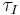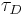) determine what the roots of the characteristic equation of the closed-loop system will be.
Process identification and parameter estimation: obtaining a dynamic process model using experimental measurements
- understand the underlying requirements when using input disturbances to obtain a process model from the process response.
- obtain a process model making use of a step input and the process reaction curve.
Simulation Project
Have a look at this page for help with common problems regarding the simulation project.
